Home     Email

Principe de fonctionnement du simulateur de billard.


 

 Page Principale
 

Objet de ce petit papier:

Le but de cette page est d'éclairer sous un jour différent quelques uns des aspects de la physique du billard et plus particulièrement dans le cadre de la modélisation sur ordinateur.
J'essaie dans cette page de capitaliser les diverses réflexions et échanges avec des joueurs, des curieux du billard et de la physique.
Les problèmes abordés sont divers et je n'ai pas la prétention d'écrire un livre sur la modélisation en général. Aussi, je vous conseille de passer très vite sur les passages traitants de choses qui vous sont familières, les chapitres sont très indépendants les uns des autres.
Bonne lecture, et n'hésitez pas à me signaler des erreurs ou des imprécisions.
 

(soyez indulgents sur les fautes de frappe ou pire, d'orthographe ... le contrôle qualité n'est pas encore passé.)
 

0) Rappels : Que cherche-t-on a faire ?

1) Architecture du Programme.

2) Phénomènes physiques mis en jeu.

3) Méthodes de résolutions.

4) Pièges, astuces, remarques


 

0) Rappels : Que cherche-t-on a faire ?

 

Un simulateur.

Au risque de me répéter (si vous avez lu les autres pages de ce site), le but de ce programme est de simuler "dans la mesure du possible" la réalité du jeu de billard.
Dans la mesure du possible prend ici le sens beaucoup plus terre à terre de "dans la mesure de mes possibilités". Je ne dispose que d'un budget "temps" limité, de connaissances limitées, et à priori, vous comme moi possédons des moyens informatiques "limités".

Par ailleurs, j'ai voulu écrire un soft qui tourne sur des machines diverses, quoiqu'assez rapides (à partir du pentium). Ceci m'a conduit à négliger certains aspects qui restent difficiles à programmer, ou qui, à mon sens n'allaient pas dans la direction voulue. Les buts de cette  réalisation sont :

Reproduire des comportements.

L'affichage est ici réduit à sa plus simple expression. Vue du dessus, pas de reflets des lampes sur les billes... Vous avez sans doute compris si vous avez lancé le programme que l'aspect graphique n'est pas ma priorité, et est nettement moins affriolant que ce que l'on trouve dans le commerce. D'un autre coté je ne fais pas cela à plein temps, et cela ne me fait pas vivre non plus. Je me suis surtout attaché à reproduire le comportement des billes. Et ce, dès le début de leur mouvement.

L'interaction entre la queue et la bille jouée est réduite au minimum. Si on met du bas, il y aura du bas, si on joue avec la queue inclinée, on simulera un massé ou un piqué, mais je ne considère pas les équations physiques qui pourraient conduire à des fausses queues ou à des glissements de la bille "autour de la queue" lors de petits massés.

Quand commence la simulation.

L'objet de ce simulateur est de modéliser le mouvement des billes. J'ai pris l'option de modéliser le plus simplement possible l'action de la queue sur la bille. Il n'y a pas de notions de talon fortement serré ou non, de procédé plat ou rond, de coup sec ou non, ou encore d'autres choses.

Pourquoi ?.

La raison principale est qu'il est très facile de deviser sur ces aspects du billard, exemples à l'appui, mais bien souvent, ces notions sont très dures, voire impossible à mettre en équation. Par exemple, dans le magnifique livre de R.Conti , le "professeur" donne le conseil de reculer le pied droit pour allonger le coup. Ça marche !.  Mais comment voulez vous formaliser ceci dans un simulateur, et physiquement ?.

Ces considérations s'appliquent à l'homme, et au mécanisme humain. Par exemple, je n'ai jamais joué au golf, mais les champions (des gens compétents) insistent très souvent sur le mouvement après le coup. Quand le club remonte. Je peux vous garantir que la balle se moque bien de savoir, une fois partie, que le geste était beau ou disgracieux une fois le choc passé. Pourtant, pour corriger certaines appréhensions, certains défauts, il faut se concentrer sur cet aspect du coup.

J'ai coutume de dire aux gens qui m'écrivent que ce simulateur est en fait un simulateur d'un robot qui joue au billard. Donnez lui 10 fois de suite la même position et les mêmes indications pour jouer le coup, il jouera 10 fois le même coup, à moins d'un micron près. Personne n'est capable d'une telle performance. Et ceux qui s'en rapprochent le plus sont les champions, qui savent évacuer l'aspect émotionnel de leur jeu, et jouer "mécaniquement". Leurs problème n'est pas "Est-ce-que je vais réussir ce petit massé ?", mais "La rouge doit elle se retrouver ici ou 1cm plus loin pour le coup suivant.".

Vous donnez des ordres à un robot. Ou, si vous préférez, vous êtes en plein rêve et quand vous mettez du bas, il y en a, quand vous visez une bille à 2m de la votre, vous l'atteignez... Bref, tout va bien.

Sincèrement, je pense que cela (l'introduction des données telles que la force du coup, la quantité de rétro, l'effet, l'angle de la queue) ne pénalise en rien l'utilisateur, une fois prévenu.
 
 

Ou trouver les équations physiques.

Cette question prend des significations différentes suivant votre sensibilité.
Si vous êtes joueurs, vous avez le laboratoire, il vous reste à chercher les lois qui se cachent derrière vos expériences.
Si vous êtes étudiant par exemple, et que vous cherchez à vérifier que ce que vous avez appris vous permet réellement de comprendre et de prévoir "la nature", alors, vous avez des lois, beaucoup de lois, mais vous hésitez à vous en servir et à savoir lesquelles sont pertinentes. Il vous manque dans ce cas la confrontation avec l'expérience.
Enfin, si vous vous retrouvez dans ces deux portraits, ou dans aucun, il vous reste la possibilité de vous en remettre à l'expérience des autres et à la connaissance générale. Au travers de rencontres, de livres ou de documentations de tous genres. Restez toutefois vigilant, et n'hésitez pas à douter. Et dans le doute à chercher à comprendre. Et si ça ne suffit pas à vous faire expliquer... Évitez quand même comme le faisait un camarade d'étude de tout remettre en cause. Certains théorèmes sont vrais... trouver  en quelques secondes un contre exemple à une affirmation établie il y a quelques siècles, utilisée par tout le monde, cela peut relever du génie, mais le plus souvent cela révèle d'autres dispositions nettement plus communes.

Les livres donc :
Vous trouverez un peu partout, dans des livres de cours de physique, ou de mécanique les équations nécessaires à la compréhension des phénomènes en jeu dans le mouvement des billes. Selon votre formation, vos souvenirs ou encore votre pugnacité si vous vous y remettez, vous constaterez que le notations dans ces ouvrages sont assez différentes les uns des autres.

Par exemple, dans l'ouvrage de Coriolis, les explications sont assez claires, mais nécessitent une lecture attentive (papier + stylo à portée de main). De plus, le traitement est assez orienté "géométrie". D'autres ouvrages beaucoup plus récents n'apportent à mon sens rien de plus. Les auteurs abordent les problèmes de la même façon, utilisent le même formalisme, et se contentent d'énumérer des phénomènes, de façon très rigoureuses, pour quelques lignes plus loin dire des choses du style, entre 10 et 20 degrés, telle ou telle quantité est négligeable.  Bel effort. Moi, j'ai 11 degrés et je suis en train de programmer ces équations sur ma calculette, je fais quoi ??

En un mot, si vous voulez un ouvrage de référence, il faudra le payer. En sous, car l'ouvrage de Coriolis est assez cher, en réflexions, car sa lecture n'est pas aisée. Mais vous ne regretterez pas si vous ne voulez acheter qu'un seul livre. Dans le cas contraire, tournez vous plutôt vers des cours de mécanique du solide.
Si vous voulez comprendre le billard, mais que vous ne voulez pas trop de physique, reportez vous plutôt sur des ouvrages écrits par des "bons joueurs". Il y en a d'excellents (des ouvrages), et ces gens la (les grands joueurs) ont souvent une intelligence certaine de la physique. Méfiez vous des ouvrages ou l'on fait référence au traité sur la "Métaphysique transcendantale des effets au jeu de billard" de G. Coriolis...
 
 

Changement de nature des phénomènes.

Les équations physiques mentionnées ci-dessus, sont issues directement de quelques principes physiques. Essentiellement les lois de Newton ceci dit en passant. La prise en compte des diverses forces sur les billes va donner des équations différentes. Non pas que la physique soit différente, mais ce qu'on cherche à résoudre l'est.
Ainsi,  une bille qui tourne sur elle même en glissant sur le tapis, est régie par une équation plus complexe qu'une bille qui roule sans glisser. Donc, une bille qui initialement glisse, et qui finalement roule, va être décrite par deux jeux d'équations. On a coutume de dire qu'à un moment donné, il y a eu changement de nature du mouvement.
Le changement de nature est encore plus violent, cette fois au vrai sens du terme, lorsqu'une bille qui roule en heurte une autre. Modéliser ce phénomène revient à décrire la trajectoire avant le choc, à calculer l'instant exact du choc, et les paramètres qui permettent le calcul des conditions initiales du mouvement après le choc.
"Informatiquement" parlant, il faut à tout moment savoir dans "quel cas" on se trouve, ou savoir prédire quand se passera le prochaine changement de nature. Ce n'est pas ce qu'il y a de plus facile.
Cela constitue même une des principales difficultés de la programmation des équations. Par exemple, si une bille glisse sur le tapis, celui ci engendre une réaction de frottement . Cette réaction de frottement va cesser á l'instant même où le glissement cessera.  De même,  la réaction de frottement va toujours faire en sorte de s'opposer au mouvement, mais ne va jamais imprimer à l'objet un mouvement "dans l'autre sens". Une des taches ardue à réaliser va donc être de décider à tout moment de la valeur de ce frottement. Et comme "à tout moment" signifie souvent en informatique, tous les "petits pas de temps", par exemple toutes les millisecondes, c'est un problème qui va revenir souvent.

Un exemple concret:
Vous roulez en voiture à 100km/h. Vous freinez, ce qui a pour effet d'imprimer á la voiture une décélération (modification delà vitesse dans le temps). Supposons que cette décélération soit de 10km/h par seconde et constante jusqu'à l'arrêt. Alors, au bout de 5 secondes, votre vitesse n'est plus que de 50km/h. De 20km/h au bout de 8 secondes.... et vous êtes à l'arrêt au bout de 10 secondes.
Bien, maintenant supposons que votre vitesse initiale est de 95 km/h. Au bout de 8 secondes vous êtes à 15 km/h, à 5 au bout de 9 secondes, ... et à 0 au bout de 10 secondes, mais ce depuis le temps t=9,5 secondes.
Une application bête et méchante de V(t) = 95 - 10 t    vous donne une vitesse de -5 km/h après 10 secondes.
Il faut donc détecter l'arrêt avec précision pour décrire le mouvement.

Transposez ceci au cas d'une bille en rotation, et vous verrez que
1) le frottement modifie la vitesse de rotation Oméga
2) le frottement modifie la vitesse de translation V
ces modifications vont dans le sens de la diminution de la vitesse de glissement VG et doivent donc être traitées en simultanément. Sinon,  on entre dans le cycle infernal, V diminue, Oméga et VG aussi, .... (la vitesse de glissement devient nulle entre deux calculs) ,  VG change de signe (la voiture recule) on modifie V et Oméga pour que VG diminue .... et ainsi de suite.

Un peu comme si vous avez le choix entre le micro-onde et le congélateur pour chauffer une casserole d'eau à une température donnée. Si vous prenez une décision (chaud ou froid) toutes les 10 secondes, vous serez moins précis que toutes les secondes, et vous allez dans les deux cas prendre le risque de dépasser la consigne dans un sens ou dans l'autre.

(ces problèmes ne sont pas des problèmes simples.)

Sources d'informations, lectures.

En ce qui concerne les livres scolaires, dans les ouvrages de physique jusqu'en terminale, vous entendrez parler de points matériels, de moments, de forces, mais avec, entre autre, des notations qui sembles inappropriées pour décrire un mouvement complexe avec des rotations autour d'axes quelconques. Vous serez en mesure de "comprendre" pourquoi une bille avec un effet rétro freine, mais il va vous manquer des outils pour calculer au bout de combien de temps elle s'arrête, et quelle distance elle parcourt en revenant vers vous. (si je me trompe, reprenez moi.) De plus, le frottement n'est souvent abordé que dans ses aspects les plus simples, c'est à dire de telle façon que l'on puisse mener à bien les calculs.

Dans des ouvrages de mécanique un peu plus complexes, vous trouverez les outils pour résoudre ces problèmes, mais toujours avec des conditions initiales assez simples.  Les notations deviennent un peu plus complexes, un peu plus lourdes à manipuler. Mais c'est nécessaire pour bien formaliser les problèmes que l'on doit savoir résoudre, et cela permet aussi de s'affranchir de plus en plus du "feeling".  Dans ces ouvrages, on apprend à résoudre des problèmes en évacuant de plus en plus l'intuition. Une phrase victorieuse est souvent du style : "c'est marrant, ça marche comme en vrai...".

Pourtant, on reste un peu sur sa faim, et on doute (quand on est élève) de plus en plus du bien fondé de tout cela quand on s'aperçoit que l'on est capable de calculer la période de la rotation des satellites de Jupiter, et que l'on ne sait pas calculer la période d'un pendule simple, quand celui ci décrit de grandes oscillations.
Calculer s'entend ici par "donner une expression (simple ou non : par exemple T=2pi sqrt(l/g))" apportant la solution pour un jeu de paramètres . On peut bien sur calculer une valeur numérique, ou encore établir des tables, ou des fonctions d'approximation par le calcul des solutions pour un grand nombre de valeurs en entrée.

Le problème est bien la. Il y a des choses compliquées qui se calculent bien, où les théories donnent à l'étudiant des équations qui se simplifient et qui à l'aide d'une calculatrice donnent des résultats du style, la période est 2.23453 secondes. Et puis, il y a tous les autres problèmes. Ceux pour lesquels on ne sait que dire des choses comme : Si le pendule fait un angle alpha avec la verticale, alors on a une force F. Cette force F donne une accélération A.
On a alors une équation du style : si on est à gauche, on freine pour revenir à droite, et si on est à droite, on freine pour revenir à gauche. On sait ce qui se passe à tout instant, et on cherche à acquérir des connaissances sur de longues durées.
 

Un exemple.

Pour imager, on cherche à faire le plan d'un circuit automobile (une route qui revient à son point de départ), en étant à l'intérieur d'une voiture, la nuit, avec des phares qui éclairent pas trop loin devant. Il faut pour cela faire quelque chose qui ressemble à : j'avance de 10 mètres, je trace un trait sur le plan de centimètre (échelle 1/1000). Je regarde si je tourne et de quel angle. Si oui, j'indique sur le plan la nouvelle direction. .... Et on recommence ...
Si vous faites cela, vous allez transformer une connaissance "locale" en une connaissance "globale". Vous connaîtrez la longueur du circuit, vous saurez le temps mis pour faire un tour suivant votre vitesse. Maintenant, vous vous rendez compte que si, au lieu de faire le point tous les 10m, vous le faites tous les mètres, le résultat est bien meilleur. Mais de combien ?...
 

Un peu de terminologie en passant.

En physique, ou en math, on appelle la démarche précédente intégrer, et les équations qui lient des variables comme la position, la vitesse et l'accélération des équations différentielles. Et la question sur la précision obtenue, suivant le "pas" d'intégration (les 10 mètres de l'exemple précédent) sont le style de question que se posent les personnes qui font des mathématiques appliquées. Ces questions concernent plus la façon de résoudre le problème que le problème lui même.

Quand on a plusieurs variables, qui dépendent les unes des autres, (de la même façon que la vitesse dépend de l'accélération, la position de la vitesse ...) on parle alors d'équations aux dérivées partielles.

On dit également que la fonction vitesse est la dérivée de la fonction position,  que l'accélération est la dérivée de la vitesse, et de façon réciproque, que pour calculer la vitesse, il faut intégrer l'accélération, et que pour calculer la position, il faut intégrer la vitesse.

Certaines équations différentielles peuvent se résoudre sans faire intervenir le calcul numérique.
Par exemple, le calcul du mouvement d'un pendule simple lors de faibles oscillations.
Parfois, on ne parvient qu'à donner une expression sous forme d'intégrale, (une formule) qui n'admet pas de primitive simple (une autre formule). On doit alors si on veut une expression numérique faire appel au calcul numérique.
Parfois encore, on ne sait pas simplement donner une expression sous forme littérale. On se contente alors de donner les équations différentielles, tout en sachant que leur résolution ne sera QUE NUMÉRIQUE. Les équations de la mécanique des fluides sont un exemple de cette démarche. On les écrit souvent en pensant très fort à leur résolution numérique.
 

Un autre exemple ?.

(Vous prendrez les valeurs numériques qui vous conviennent, celles ci sont farfelues).

Un "couple" de lapins donne naissance a 3 petits tous les mois.  Les lapins peuvent se reproduire dès qu'ils ont 2 mois. Combien avez vous de lapins au bout de 1 an ?. Maintenant, la même question en considérant qu'un  lapin a une durée de vie de 6 mois. Pas facile ??.
Réfléchissez à ces problèmes et vous verrez apparaître des équations différentielles.
Essayez de les résoudre et vous verrez qu'il manque une donnée très importante pour l'application numérique. Le nombre de lapins au début. C'est ce que l'on appelle la condition initiale.
Vous verrez aussi qu'il est très facile de calculer combien il y aura de lapins le mois suivant, connaissant la population actuelle, mais que c'est nettement plus compliqué de calculer la population après un nombre de mois élevé. Si vous avez un ordinateur, ou une calculatrice programmable, vous pouvez résoudre ce problème "sans trop de réflexion", vous calculez les données de mois en mois.
Vous verrez aussi que commence à intervenir des problèmes numériques, (des grands nombres) et que si on vous demande de calculer la population après 1 million de mois, ....,  l'ordinateur va tourner un certain temps.

Voilà. Vous avez une petite idée de la résolution numérique d'un problème "localement" très simple (passage du mois n au mois n+1).

Si vous fouillez un peu, vous verrez qu'il existe des équations différentielles pour lesquelles les conditions initiales sont si importantes qu'une variation infime sur un des paramètres donne des comportements complètement différents.  Mais tout ceci est une autre histoire. (lisez le livre de Gleick sur la théorie du chaos, (mais n'en "mettez" pas partout ... du chaos). C'est un bon ouvrage de vulgarisation. Les gens à qui le l'ai passé l'ont bien aimé.).


 
 

1) Architecture du Programme.

Interface graphique, gestion des options...

Ce paragraphe concerne l'introduction des conditions initiales qui vont permettre d'initialiser le mouvement des billes. J'ai essayé de rendre l'interface utilisateur la plus conviviale possible, et surtout de faire en sorte que la dextérité n'intervienne pas dans le calcul des trajectoires. Donc, on ne simule pas le mouvement de la queue avec la souris, et il n'est pas nécessaire d'avoir une très bonne vue pour jouer une finesse.

Les objectifs que je me suis fixé pour l'interface graphique sont :


En ce qui concerne la gestion des options, du travail reste à faire. Entre autre, la possibilité de régler des paramètres comme les divers frottements, la taille du billard, ...  Ces options permettront de mieux apprécier les phénomènes physiques en jeu lorsqu'elle seront dans le soft. Par exemple, de vérifier l'influence d'un tapis neuf par rapport à un tapis ancien, de bonnes bandes, la température etc... Ceci représente beaucoup de travail de modélisation, et devrait répondre à la plupart des critiques qui me sont faites sur le réalisme de ce simulateur.
En donnant la possibilité de modifier la façon de répondre du billard, je devrais m'approcher de plus en plus de ce que vous voyez sur "votre" billard, non ?
 

Saisie des conditions initiales.

Comme je l'ai dit auparavant, j'ai décidé de faire l'impasse sur le problème "choc Queue/Bille". Je ne sais pas formaliser ce problème d'une façon satisfaisante, et "restituer" les paramètres que sont le poids de l'avant bras, le mouvement du poignet, la position du corps, la forme du procédé de façon satisfaisante.
L'interface que je propose est un peu plus agréable que la donnée sous forme numérique de la vitesse de la bille 1, ainsi que son axe de rotation et sa vitesse angulaire, mais le principe reste le même, vous entrez sous forme graphique ces données (les vitesses de la bille 1), et non les conditions initiales d'un choc (vitesse de la queue, localisation de l'impact...) qui sera analysé pour donner ces valeurs. Suis-je Clair ?.
 

Modélisation des objets.

On a trois billes. Et un billard. Comment représenter ces objets dans la mémoire de l'ordinateur. Comment représenter le temps, et l'espace dans lequel évoluent ces billes. C'est l'objet de la modélisation. Pour faire une analogie, si vous cherchez à modéliser la formation des bouchons sur une route, le fait que les voitures aient 4 roues importe peu. Par contre, la vitesse de réaction des conducteurs est importante. Si vous calculez la déformation lors d'un choc, la modélisation des voitures devra être beaucoup plus fine... A chaque problème, sa modélisation.

Ici, le modèle du billard est un plan, délimité par des bandes, et des billes sphériques. Chacun de ces objets possède des caractéristiques qui sont  principalement :

Pour le billard:

Pour les billes: Pour les bandes:


A noter que tout mouvement d'un solide, aussi complexe soit il, peut être à tout moment décrit par la donnée de son vecteur rotation (axe + vitesse angulaire), et la vitesse d'un des points du solide. On dit parfois que tout mouvement est localement tangent à un mouvement hélicoïdal (rotation + translation).

Comme on le voit, les objets sont très "grossièrement" modélisés. Et le nombre de variables qui servent à décrire un état est limité. Heureusement, car on aura pas mal de calculs à faire.

La modélisation de phénomènes est tout un art. Et aussi une démarche d'esprit. Quand vous voyez quelque chose autour de vous, et que vous vous posez la question, "comment pourrais-je simuler cela ?", vous êtes amenés à tenter de comprendre comment ça marche. Et bien souvent, cette réflexion amène a un compréhension profonde des phénomènes. (Un exemple, comment modéliser la formation des bouchons sur un autoroute ?.)
Mais attention, une mauvaise modélisation conduit à de faux modèles. Essayez d'imaginer par exemple ce que serait un simulateur de billard dans lequel on ne considérerait pas la rotation des billes, mais le frottement dans l'air. Certains phénomènes sont négligeables, d'autres pas.

L'idéal est de disposer de langages de programmation et de structures de programmes qui permettent de "débrancher" tel ou tel traitement. Par exemple pour vérifier le bon comportement des chocs, et pour mettre au point cette portion de programme, si on peut inhiber les autres traitements, comme les frottements divers et la perte d'énergie sur les bandes, on va pouvoir regarder des billes (des "palets") qui s'entrechoquent pendant longtemps, puisque la perte d'énergie est nulle.

C'est pourquoi il faut toujours être critique, et ne pas hésiter à remettre en cause ses modèles, et à prévoir "de la place" dans l'architecture du programme. De ce point de vue, des langages objets comme le c++ sont biens pratiques, car on peut assez facilement modifier des comportements sans rendre le programme trop incompréhensible.
 

Interactions.


On a les objets, en fait,  les modèles des objets.  Maintenant, il faut modéliser les interactions entre ces objets. On s'aperçoit que les phénomènes en jeu sont essentiellement :

Les équations sont assez classiques, et ne nécessitent que peu de bagage scientifique, mais par contre beaucoup de rigueur d'écriture. Surtout si on décide de porter un jour le code du bloc papier ou du rétro-projecteur à une machine. La, ça ne pardonne pas, l'erreur de signe a des conséquences visibles. Assez surprenantes parfois.

Donc, pas de problèmes trop complexes sur le traitement de ces chocs, et du frottement.

Ce qui est difficile à traiter, et j'y reviendrai plus longuement sur des exemples, c'est le changement de nature des phénomènes en cours de mouvement.

Un exemple, lorsque deux billes se rencontrent, il faut calculer exactement la position au moment précis du choc. Simple quand une bille est à l'arrêt et que l'autre se déplace en ligne droite. Un peu plus délicat quand les deux sont en mouvement et décrivent des trajectoires complexes. (au passage, le fait que les trajectoires se coupent ne signifie pas qu'il y a choc. Pour qu'il y ait choc, il faut que la distance entre les billes soit à un instant donné inférieur à un diamètre de bille. )

Un autre exemple sur lequel je reviendrai, lorsque la bille glisse sur le tapis, elle est soumise à une force de frottement qui tend à s'opposer au glissement. Après un certain temps, elle se met à rouler. A cet instant précis, le frottement disparaît. Le mouvement change de nature.

Un autre problème se dessine alors. Celui du temps de calcul. Il va falloir à tout instant détecter ces collisions et ces passages par le roulement. Mieux vaut faire une routine de calcul rapide.
 
 

Visualisation des trajectoires.

Le but du jeu reste quand même de produire des résultats de calculs compréhensibles, et sous une forme agréable. On va donc afficher les trajectoires des différentes billes et leur évolution dans le temps. L'option prise ici est de réaliser tous les calculs et de n'afficher les trajectoires qu'après. Mais il existe d'autres façons de faire. On peut également réaliser les calculs à la volée: Calculer ce qui se passe pendant les quelques prochaines millisecondes, puis l'afficher. Et recommencer jusqu'à arrêt complet des billes.

Ces deux techniques ont leurs avantages et leurs inconvénients. La première version du simulateur (windows 3.1) faisait les calculs et l'affichage en même temps. Aujourd'hui, je fais d'abord tous les calculs, et l'affichage ensuite.

Sous forme synthétique, je vous présente selon moi les avantages et les inconvénients de ces deux méthodes:
 
 
Méthode Affichage différé: Affichage pendant les calculs
     
Avantages Algorithme plus simple. Moins d'attente sur un machine lente entre deux événements.
On peut sur des machines lentes à la fois: 
diminuer la fréquence du rafraîchissement, 
et augmenter les pas de temps d'intégration.
  Les calculs sont toujours menés de la même façon. 
Les résultats sont reproductibles d'une machine à l'autre.		 Nettement plus marrant à écrire. Il faut synchroniser des taches, mettre en place des heuristiques pour déterminer les diverses fréquences. 
Faire glisser ces fréquences en temps réel pour tenir compte de la charge machine... 
  Possibilité de rejouer le même coup sans devoir refaire le calcul. 
Par exemple pour des zooms, des redraws...		  
----
-------
--------
Inconvénients Attente avant l'affichage sur des machines lentes.
Il ne se passe rien à l'affichage pendant le calcul. 		 Deux conditions initiales sur des machines très différentes peuvent donner des résultats différents. 
Les calculs ne sont pas les mêmes selon la vitesse de la machine. 

Certaines personnes m'ont signalé un mouvement un peu rapide des billes, et un freinage un peu brusque. Ce problème est du à la synchronisation entre le temps physique avec lequel les calculs ont été effectués, et le temps de l'affichage. Tout se passe en fait comme si le film du mouvement des billes était passé en accéléré. Essayez sur votre magnétoscope de visionner un coup de billard, et vous retrouverez ce comportement. Il faut en fait que je donne la possibilité de corriger autour d'une valeur raisonnable le ratio entre le temps "affichage" et le temps physique.  Cela réglera le problème et permettra aux possesseurs de cartes très rapides d'augmenter le taux de rafraîchissement.


 

2) Phénomènes physiques mis en jeu.

Les chocs

Il y a deux types de chocs à étudier ici. Les chocs entre deux billes, et les chocs entre une bille et une ou plusieurs bandes (cas du choc dans un coin).
 

.../  A COMPLÉTER   EN CHANTIER
Conservations diverses (énergie, Qte de Mvt) ...
../...

exemple d'avantage de l'utilisation du référentiel barycentrique.
 
Referentiel Barycentrique

Les deux billes se dirigent l'une vers l'autre. Si à chaque instant on désigne le centre de gravité des deux billes, on voit (et on prouve) que si les billes se déplacent en ligne droite, à vitesse constante, le centre de gravité, lui aussi se dirige en ligne droite.  Il y a de nombreuses curiosités dans le repère barycentrique, ainsi la somme des quantités de mouvements (vitesse x masse) est nulle. Et ce à tout moment. Et bien d'autres choses faciles à démontrer. 

Par ailleurs, on montre que lors d'un choc sans frottement (bonne approximation, le coefficient de frottement entre deux billes est très faible, et il sera possible de simuler l'effet d'engrenage après avoir résolu le choc), la vitesse tangentielle est conservé, seule la vitesse normale subit une discontinuité. Les directions tangentielle et normale se rapportent au plan tangent aux billes lors du choc.

Il y aura contact si la distance a un instant donné entre les deux billes est plus petite qu'un diamètre. C'est simple non ?. 
J'espère vous convaincre avec le dessin suivant qu'il n'en est rien. 
 

Detection du choc
Sur ce schéma, une bille animée d'une vitesse dont la direction varie va peut être rencontrer une bille immobile. Si le pas de temps d'intégration est assez grand, on se retrouve avec une situation comme représentée sur le dessin. On calcule des positions tous les "dt", et le choc peut se produire entre deux positions. (entre t et t+dt). Il faut donc dans ce cas, trouver une solution, soit pour prédire qu'il risque d'y avoir bientôt un choc, soit pour "reculer" dans le temps une fois qu'on sait qu'il y a eu choc. 

On pourrait se poser la question : est-ce bien nécessaire de calculer avec autant de précision l'instant du choc ?. C'est nécessaire si on veut jouer correctement des "coups durs", ou des coups très rapides. Je reviendrai sur ces aspects plus loin. 

Le cas représenté ci-dessus est encore un cas simple. On peut avoir deux billes qui décrivent des trajectoires non linéaires. Détecter les chocs devient dans ce cas une part importante des calculs à chaque itération. 

 


 

Les frottements

On distingue plusieurs type de frottements. Les deux principaux sont le frottement fluide et le frottement solide. La différence essentielle est liée à l'apparition ou non de la force de frottement. Le frottement fluide ne se manifeste que si il y a mouvement. Par exemple, le frottement dans l'air. Il n'y a frottement sur un corps que si ce corps se déplace par rapport à l'air environnant.  Le frottement solide, lui se manifeste même entre deux objets même s'ils sont  immobiles l'un  par rapport à l'autre. Le frottement fluide peut également voir son intensité varier avec la vitesse, linéairement ou avec des lois plus compliquées.

Dans les deux cas, le frottement est une force qui s'oppose au mouvement, ou qui empêche ce mouvement si les objets sont initialement à l'arrêt. Le frottement dissipe en fait de l'énergie, le plus souvent sous forme de chaleur.
On distingue encore dans ce que l'on appelle frottement solide plusieurs types de frottements.


 
 
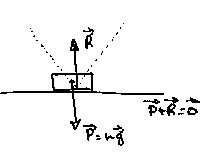Un objet est posé sur un plan. En pointillé est représenté le cône dans lequel la réaction du plan doit rester. 
Le demi angle de ce cône est l'angle alpha tel que tangente(alpha)=mu. mu étant le coefficient de frottement à sec. 

 
 
 
 
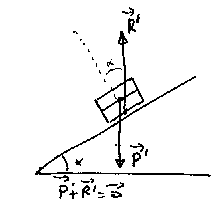Le même problème, cette fois ci sur un plan incliné. 
Dans les deux cas, la force de réaction fait un angle inférieur ou égal à la valeur limite.

Si 'objet est plus lourd, la réaction fait toujours le même angle avec la normale au plan. Seule l'angle entre la réaction et la normale au plan incliné ne change pas


 
 
 
 
 
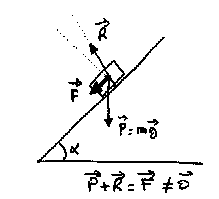Maintenant, l'angle du plan incliné est supérieur à l'angle max. du cône de frottement. La réaction fait un angle avec la normale au plan égal à l'angle de frottement. La somme (vectorielle) des deux forces (poids et Réaction) est une force dirigée vers le bas et parallèle au plan. Le solide glisse. 

A noter que des que le mouvement apparaît, la réaction va passer de l'angle maximal autorisé par le frottement statique à l'angle max. autorisé par le frottement à sec.


 
 
 
 
 
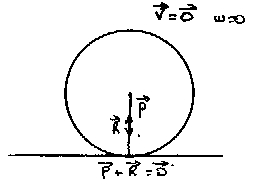Une bille posée immobile sur un plan. La réaction du plan passe par le centre de gravité de la bille. 
La résultante (somme vectorielle) P+R est nulle : pas de mouvement.

 
 
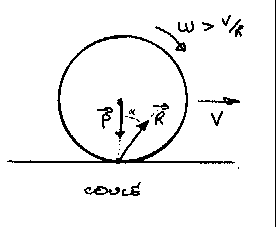Un coulé. 

La vitesse de rotation de la bille est supérieure à la valeur de roulement qui vaut V/R. 

La vitesse du point de la bille en contact avec le sol est dirigée vers l'arrière. La force de frottement est opposée en direction à la vitesse de glissement, donc dirigée vers l'avant. 

R est tel que en projection sur un axe verticale, elle s'oppose au poids P, et fait un angle alpha (dont la tangente vaut le coefficient de glissement à sec) avec la normale au plan de contact.
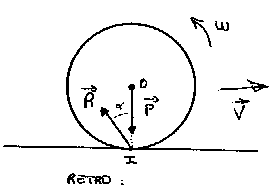Cette force contribue à augmenter la vitesse, et à freiner la rotation.
 

 Un rétro.

même explication que pour le coulé. 

Un point important à noter toutefois. J'ai dit que le frottement tendait toujours à s'opposer au mouvement. Or dans ces exemples, et plus particulièrement pour le coulé, on peut croire que le frottement a un rôle "moteur". Il n'en est rien. Le fait est que le frottement freine ici le mouvement de rotation, et transfert une partie de cette rotation en translation. Mais globalement, il y a dissipation d'énergie

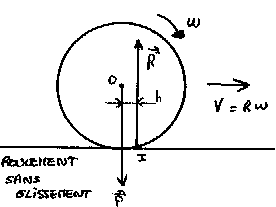 Ça roule. 

Le roulement de glissement se manifeste sous la forme d'un couple qui tend à freiner la rotation. La vitesse "linéaire" s'ajuste de telle façon à ce qu'on ait toujours un glissement nul. 

Donc le couple fait baisser Oméga.  Et comme V est contrainte à rester égale à Oméga x Rayon, V diminue elle aussi. 


 
 

Quelques valeurs du coefficient de frottement sur des matériaux secs, juste pour donner l'ordre de grandeur.
Vous trouverez des valeurs "exactes" pour de nombreux matériaux dans des conditions diverses (mouillé, graissé) dans des formulaires techniques (Par exemple le GIECK).

On distingue les deux coefficients de frottement dans le tableau ci-dessous:
(j'essaierai de compléter ce tableau lorsque j'aurai d'autres valeurs).
 
 
Matériaux Coeff. glissement Coeff. adhésion
Bois / Bois 0,15 ... 0,4 0,4 ... 0,6
Pneu / Asphalte 0,5  ?
Pneu / Béton 0,6  ?
Téflon / Téflon 0,04  ?
     

Et quelques valeurs du coefficient de roulement:
 
Matériaux Bras de levier de la résistance 
au roulement en mm
Pneu / asphalte  0,10
Pneu / Béton 0,15
acier / acier 0,005 ... 0,01
bois / bois  0,8

 
 

Autres. Frottement "de pivotement".


Un frottement que nous n'avons pas considéré, mais qui reste important pour bien décrire le mouvement d'une bille de billard, est le frottement de pivotement de la bille. A savoir, le couple résistant qui s'exerce sur la bille lorsque celle ci tourne sur elle même comme une toupie.
Si on n'en tient pas compte, cela revient a dire que l'effet (droite ou gauche) que l'on applique à la bille lors du choc Queue/Bille reste invariant lors du mouvement. En effet, la réaction du tapis est une force horizontale (dans le plan du tapis), et ne contribue pas au changement de la composante verticale du vecteur rotation.
Une bille mise en mouvement avec un effet à droite ou à gauche voit cet effet diminuer au fil du temps. Cette diminution n'est pas exprimable si on ne tient compte que du glissement "linéaire" du point de contact entre la bille et le tapis. Voici donc une première entorse aux équations physiques simplifiées utilisées pour décrire le mouvement.
Il faut introduire un terme correctif, ou alors introduire une nouvelle loi dans nos équations.

3) Méthodes de résolutions.

Énoncé du problème.

Je vais essayer de vous décrire un peu plus en détails la façon d'intégrer numériquement une équation différentielle. Pour cela, je vais m'appuyer sur un exemple concret, et pas trop compliqué.
Il existe de nombreuses méthodes et je ne vais vous décrire ici que la plus simple, car, d'une part, c'est la plus intuitive, et d'autre part, elle est très souvent suffisante pour des applications réelles. Sachez toutefois qu'il existe de nombreuses discussions théoriques sur ces sujets, et que de nombreux schémas beaucoup plus élaborés existent et permettent des améliorations non négligeables du temps de calcul et de la précision. Reportez vous à des ouvrages d'analyse numérique si vous désirez plus de renseignements.

Tant qu'a faire, on va choisir de modéliser un phénomène simple, mais dont les équations ne s'intègrent pas formellement. (i.e. on ne peut pas trouver de formule générale.)

Un pendule simple.

Soit un pendule constitué d'une tige de masse négligeable, de longueur L, accrochée à un point fixe O, et à laquelle on suspend une masse ponctuelle M.

On écarte la masse d'un angle Alpha avec la verticale, et on veut calculer le temps mis par la masse pour revenir à la verticale du point O. (la demi période).

Écrivons les équations.

Si alpha est l'angle de la barre avec la verticale, g, l'accélération de la pesanteur, alors :

M g L sin(alpha) = - (M L**2) d**2 / dt**2 (alpha)

(M L**2 , lisez M L au carré) est le moment d'inertie du pendule au point O
d**2 / dt**2 (alpha) est l'accélération angulaire (lisez :  d 2 alpha sur d t 2 )

Ceci est l'écriture de la relation fondamentale de la dynamique appliquée à un corps en rotation.

Si on considère que alpha est petit, alors on peut approximer sin(alpha) par alpha, et l'équation a pour solution générale:

alpha(t) = alpha0 * cos (omega * t + phi)

ou alpha0 et phi sont fixes par les conditions initiales. Par exemple, si le pendule est lâché sas vitesse initiale d'un angle A, au temps t=0, alors on écrit
alpha(0) = alpha0 * cos(phi) = A    et   d/dt (alpha(t)) = - omega alpha0 sin(phi) = 0
ce qui donne :  phi=0  et  alpha0 = A.

Maintenant, si alpha peut être amené à devenir grand, cette approximation n'est plus valable.

Nous allons linéariser le problème, en partant du principe qu'entre deux intervalles de temps dt, alpha va peu varier. Ainsi, on va approximer la courbe alpha(t) en une succession de petits segments de droite,  alpha(t0)->alpha(t1)  puis alpha(t1)->alpha(t2) ....
On va prendre t0=0, t1=dt, t2=2*dt....
Si dt tend vers 0, la longueur de nos petits segments de droite tend vers 0, et la ligne brisée ainsi constituée tend vers la courbe alpha(t).
Tout ceci est très intuitif, mais les justifications mathématiques existent et demandent de la rigueur et du savoir faire. (Hors de notre propos).
 
 

Résolution numérique


Allons-y : Pour rendre les choses plus "physiques", je vais faire appel à un "computeur", et je vous livre le programme informatique que j'écris en ce moment même sur ma calculette. (Casio FX-850)

On est en radians...

10 INPUT "A="; A : A=A*PI/180
20 INPUT "DT=";DT
25 G=10: L=10
30 ALPHA=A : T=0 : OME=0

90  REM ***** Boucle principale
100 ACC=-G*SIN(A)/L
110 OME=OME+DT*ACC
120 ALPHA=ALPHA+OME*DT

140 REM **** Test d'arret
150 IF(ALPHA<0) THEN GOTO 200
160 T=T+DT
170 GOTO 100

200 REM **** Impression u resultat : 1/4 periode
210 PRINT "T=";T
215 PERIODE = 2*PI*SQRT(L/G)
220 PRINT "Ecart : ";T- 0.25 * PERIODE;
230 END

Avec ces valeurs : L/G = 1 , la période théorique est 2PI. Le mouvement que l'on décrit ici fait un quart d'une période, on devrait donc trouver T=PI/2. Ce que l'on trouve, mais après un temps très très long si on choisit une bonne précision (un dt petit).

Voici les résultats obtenus : pour différents angles, et les écarts avec le résultat théorique de PI/2.
PI/2 vaut a peu près : 1.57079632...
 
 
Angle initial (degrés) 0.1 1 10 60
dt=0.01 1.57 1.57 1.57 1.69
dt=0.001 1.571 1.571 1.574 1.686
dt=0.0001 1.5708 1.5708 1.5738 1.6858
dt=0.00001 1.5708 1.57083 1.57379 1.68575

J'aime autant vous dire que je n'ai pas utilisé la calculatrice pour faire ce tableau.
Lorsque le pas de temps est 0.00001, et que la mesure est 1.68575, cela signifie que l'on a fait 168575 itérations. Ce n'est rien sur un pc, mais il faut quand même faire attention.

Que nous apprend cet exemple:
Primo, que l'approximation pour les petits angles est plutôt bonne.
Secundo, que pour des grands angles, il faut vraiment faire attention avec cette approximation.
Tertio, que ce problème s'intègre bien. Quand on augmente la précision, on augmente le nombre de chiffres significatifs, mais sans converger vers des résultats différents. Ce ne sera pas toujours le cas avec tous les problèmes.
 

Il existe en effet des catégories de problèmes pour lesquels en déca d'un certaine précision, on ne peut absolument pas garantir que les résultats de calcul ont le moindre sens. Méfiance donc.

Le conseil que je vous donne est de toujours tester vos résultats sur des cas simples, reproductibles, et ce avec des pas d'intégrations différents, et ci possible avec des méthodes différentes. Méfiez vous aussi des pas de temps trop petits, car parfois, on ne fait que cumuler (intégrer) les erreurs de calcul....
 
 

Autres méthodes de résolution

Dans l'exemple précédent, le schéma numérique adopté est un schéma très simple. On considère qu'entre 2 instants t et t+dt, l'accélération ne varie pas, que la vitesse ne varie pas et on écrit naturellement :

Accélération(t) = (Vitesse(t+dt) - Vitesse(t)) / dt
Vitesse(t) = (Position(t+dt) - Position(t)) / dt

ce qui donne, connaissant l'accélération au temps t,

Vitesse(t+dt) = Vitesse(t) + Accélération(t) * dt
et
Position(t+dt) = Position(t) + Vitesse(t) * dt

Comme on le voit sur ces relations, on déduit les nouveaux paramètres du système au temps t+dt en fonction des paramètres en t. On progresse de proche en proche de cette façon pour calculer ce qui se passe au temps T, en partant de la connaissance des paramètres en To=0.

On peut se poser quelques questions:

1) Pourquoi ne pas tenir compte pour calculer ce qui se passe en t+dt de ce qui s'est passé aux temps t, t-dt, t-2dt ...
Intuitivement, on a l'impression que les formules seraient plus "exactes".
2) Pourquoi "regarder" toujours en arrière dans le temps pour calculer ce qui va se passer. Est il possible de "prédire" ce qui va se passer, puis de corriger ensuite cette prédiction ?
3) Peut on aller vite quand "ça va tout droit" et freiner "quand on prend des virages" ?

Les mathématiciens, dont le domaine est le calcul numérique, ont depuis longtemps apporté des réponses à ces questions sous la forme de schémas numériques plus ou moins complexes.
Par exemple, la relation (Vitesse(t+dt) = Vitesse(t) + Accélération(t) * dt) est une relation linéaire en dt, ce qui revient à dire qu'au temps t, on calcule la vitesse en t+dt (on dessine la courbe Vitesse(t)) en prolongeant cette courbe par un segment de droite dont la pente est donnée par Accélération(t).
Il existe des schémas plus précis où cette fois, on ne considère plus la droite tangente à la courbe, mais la "parabole tangente" à la courbe.

La question 2 a conduit à l'écriture de schémas dits "prédicteurs correcteurs", où on va tenter à chaque pas de temps de corriger l'erreur en répondant à des questions du style : A-t-on été trop optimiste, ou trop pessimiste. La réponse  à cette question va conditionner les calculs pour les pas de temps suivants.

La question 3 est liée aux précédentes, en effet, plus on colle à la courbe que l'on cherche à construire, plus on peut aller vite sans commettre d'erreur, et si on dispose de prédicteurs et de correcteurs, il est possible de de poser des questions du style "est-ce que là, j'ai pas été un peu vite". Répondre à cette question revient à se donner la possibilité de reculer un peu et d'avancer plus doucement. Donc de régler sa vitesse.
 

Maintenant, pourquoi et quand se pose t'on ces questions?
Principalement quand on cherche à calculer des phénomènes complexes. Car alors, de nombreux calculs sont requis à chaque pas de temps, les pas de temps sont petits, et alors, calculer ce qui va se passer dans 2 secondes, lorsque le pas de temps est de 0.000001 seconde revient á faire des millions de calculs. (imaginez un peu au passage la complexité des modèles de la météorologie nationale !). Dans ces cas, tout ce qui peut revenir à augmenter le pas de temps sans perte de précision est le bienvenu.
Mais j'aime autant vous dire que ce gain de temps se paye en complexité des schémas....
 

Si des personnes sont intéressées, je donnerai sur le même exemple du pendule simple, des schémas plus "sexy", et les comparaisons en temps de calcul pour une même précision.

Retenez quand même que le choix d'un schéma numérique est quelque chose d'annexe dans notre cas. Si un schéma simple donne les résultats attendus, et qu'il est trop lent, alors on peut agir. Se casser la tête avant d'avoir un "truc" qui marche est une perte de temps et d'énergie. Sauf si vous êtes "numéricien".

4) Pièges, astuces, remarques

Ce que l'on peut négliger.

Ce que je vais dire ici va certainement m'attirer de nombreuses remarques (toutes proportions gardées), et décevoir certaines personnes. J'espère en contre partie que cela va rassurer ceux qui veulent réaliser des simulateurs de billard ou d'autres choses encore.

Vous vous êtes fixe un but qui est par exemple de simuler la formation des bouchons en accordéon sur un autoroute, ou la dynamique d'un champ d'étoiles, ou encore que sais-je, le mouvement de billes sur un billard. Vous avez établi tant bien que mal les équations qui régissent ces phénomènes.
 
 

Vous avez écrit sur le papier les équations:

 

* Des chocs

Vous savez connaissant les vitesses (linéaires et angulaires) de deux billes juste avant un choc, les vitesses prises par ces billes après le choc. Mais vous avez des doutes.
Comment traduire l'effet d'engrenage entre les billes ?
Le choc est il bien élastique? Et si non, quelle quantité d'énergie est perdue ?
Et si les lois du choc élastique ne s'appliquaient pas ?
 

* Du frottement


Vous avez fait la distinction entre le frottement de cohésion et le frottement à sec. Parfait. Vous avez introduit le frottement de roulement. Vous avez même pense à tenir compte du sens du mouvement pour reproduire la différence de frottement selon le sens des fils du tapis. Excellent. Au passage, tout ceci vous éloigne à tout jamais de la belle trajectoire parabolique qu'est censée parcourir la bille qui ne roule pas, puisque cette trajectoire parabolique est le fruit de calculs menés avec des hypothèses beaucoup plus simples.
Vous avez bien sur tenu compte du fait que lorsqu'une bille tourne sur elle même, il faut tenir compte d'un frottement particulier qui représente le frottement de la partie de la bille en contact avec le tapis. Adieu le contact ponctuel grâce à qui une bille tournerait comme une toupie éternellement puisque la vitesse du point de contact Bille/Tapis est nulle...
 

* Des rebonds


Vous avez tenu compte de l'écrasement des bandes qui fait que plus on tape fort sur une bande, moins celle ci restitue l'angle d'arrivée. Vous avez même tenu compte du fait que les bandes sont différentes au milieu du billard et prés des coins où elles sont moins usées. Parfait.
Quand aux rebonds successifs d'une bille sur le tapis, il est vrai que ne pas en tenir compte rend les coups de billard artistique difficilement concevable.
 
 

Sincèrement, si vous vous faites toutes ces remarques, je doute que le simulateur ne dépasse un jour le stade du projet. Non qu'il ne faille pas en tenir compte, mais ceci doit se faire graduellement, et dans la limite du raisonnable.
Ensuite, présentés tels quels, je doute que les phénomènes que je viens de mentionner soient "simulables". Tout ceci est bien trop complexe et nécessiterait des mois (années) de labeur. Pour parvenir à quoi ?. Certainement pas à un simulateur, mais à un monstre de calculs.
Un peu comme ci le moteur de Flight Simulator était le modèle informatique qui a servi à valider le dernier boeing....

Vous voulez ma façon de voir les choses ?


Ceci dit, bon jeu, et si ces quelques pages ont éveillé chez vous l'envie de vérifier sur un billard que la physique est respectée, si vous regardez maintenant le balancier de votre horloge avec un regard plein de respect et d'attention, ou si l'envie de voir des choses faites par vous sur votre pc vous démange, j'en suis heureux.
 


 
 

Bibliographie


Je n'ai pas de livre "marrant" sur la simulation sur ordinateur à vous conseiller. J'en ai cherché, pas trouvé. Sinon, en livres de cours:
- Les livres de mécanique de prépa, j'adorais tous les "Lumbroso". (Mon préféré reste quand même la Thermodynamique.)
- Les livres de mécanique pour DUT BTS
- Des ouvrages de mathématiques appliquées. Souvent ces ouvrages ne donnent que les différentes façons de résoudre numériquement les problèmes. Et la tache est déjà énorme. Il manque à mon sens dans de nombreux livres, des exemples concrets. Par exemple un bête programme en basic pour simuler un pendule double....

Si vous êtes curieux, que vous n'avez pas de librairie universitaire à portée de bus, et que vous aimez regarder avant d'acheter, je vous conseille ces quelques livres qui me semblent très intéressants sur ces sujets et qui traitent de nombreux problèmes, pas cher, très bien faits et disponibles partout :